Дистанційне навчання з 12.03 по 03.04.2020р.
Алгебра
12.03.2020 р.
Тема: Сума п-членів арифметичної прогресії ( 2 уроки)
Опрацювати п.17 стор. 166-168.
Переглянути відео урок за посиланням: https://www.youtube.com/watch?v=yfW5roC1AScВиконати №17.2, №17.6, №17.10, №17.14. Завдання виконати до 19.03.2020 р.
Геометрія
17.03.2020р.
Тема уроку: МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО(2 уроки)
Опрацювати п. 15 стор. 129-132.
Переглянути відео уроки за посиланням: https://www.youtube.com/watch?v=u8QuqShFE_E ;
https://www.youtube.com/watch?v=-dZNwtlctDA
Виконати №15.11, №15.15, №15.17, №15.20, №15.23, №15.25,№15.32. Завдання виконати до 24.03.2020 р.
АЛГЕБРА
19.03.2020 Р. ( 2 УРОКИ)
1 УРОК
ТЕМА УРОКУ: РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Самостійна робота
№1. Знайти а5, якщо а1 = 20 і d = 3.
а) 35 б)8 в) 32 г) ін. відпов.
№ 2 Знайти десятий член арифметичної прогресії:  ; -1; -
; -1; -  ...
...
а) -5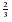 б)-11
б)-11 в)-11
в)-11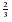 г) ін. відпов.
г) ін. відпов.
№3. Знайти а1 і d, якщо а4=10; а13= 64.
а) а1 = - 8; d=6; б) а1 =28; d= - 6;
в)а1 = - 5; d = 5 г) ін. відпов.
№4. Знайти Sзо, якщо а4=33; а15=88.
а) 2615 б) 2715 в) 2315 г)ін. відпов.
№5. Скільки від’ємних членів містить арифметична прогресія: -4,1; -3,6; -3,1;…
а) 8; б) 9 в) 10 г) ін. відпов.
6. Сума трьох чисел, що становлять арифметичну прогресію дорівнює 15,а сума квадратів цих чисел дорівнює 93. Знайти ці числа.
Шановні учні сфотографуйте виконану самостійну роботу і надішлить на цю електронну адресу o.nebulutsia@gmail.com
2 урок
ТЕМА УРОКУ:ГЕОМЕТРИЧНА ПРОГРЕСІЯ, ЇЇ ВЛАСТИВОСТІ
Опрацювати п.18 стор. 173 - 178.
Переглянути відео уроки за посиланням:
https://www.youtube.com/watch?v=IfLxdFJvcUI
Розглянути приклади розв'язуваних задач у відео.
Завдання виконати до 26.03.2020 р.
Геометрія
24.03.2020 р. (2 уроки)
1 УРОК
ТЕМА УРОКУ: РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Самостійна робота
Дано точки А (-2; 3), В(1;-1), С(2;4). Знайдіть:
а) Координати вектора АВ і вектора СА;
б) Модулі вектора АВ і вектора СА;
в) Координати векторa МN=3АВ - 2СА;
2. Накресліть трикутник АВС. Побудуйте: суму векторівАС+СВ; різницю векторів ВС - ВА.
3.При якому значенні k вектор а(2;6) колінеарний вектору в(-3;к) ?
Шановні учні сфотографуйте виконану самостійну роботу і надішлить на цю електронну адресу o.nebulutsia@gmail.com
2 урок
ТЕМА УРОКУ : СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ
Опрацювати п 16 стор. 141 - 145 .
Переглянути відео уроки за посиланням:
https://www.youtube.com/watch?v=yssg8G1HyQ4
Розглянути приклади розв'язуваних задач у відео.
Завдання виконати до 31.03.2020 р.
АЛГЕБРА
26.03.2020 Р. ( 2 УРОКИ )
ТЕМА УРОКУ: РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Повторити тему " Геометричеа прогресія", формули n-го члена, знаменника геометричної прогресії, властивість геометричної прогресії.
Переглянути відео урок за посиланням:
https://www.youtube.com/watch?v=lWqIxdfd3XU
Розглянути приклади розв'язуваних задач у відео.
Виконати №18.9, №18.5, №18.7 , №18. 28.
Завдання виконати до 02.04.2020р.
Геометрія
07.04.2020 р. ( 2 уроки)
ТЕМА УРОКУ: РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Я пропоную вам подивитись відео, де розв'язуються задачі.
Переглянути відео уроки за посиланням:
https://www.youtube.com/watch?v=VYxT7aMbkV4/
https://www.youtube.com/watch?v=o9dN31IVVVw
Виконати № 8, №11, №12 стор.151-152.
Повторити п. 12 - 15
Це є підготовка до контрольної роботи. Контрольна робота на наступному уроці по темі " Вектори на площині".
Ще не всі учні прислали самостійні роботи. Присилайте!
Алгебра
09.04.2020 р. (2 уроки)
1 урок
Тема: Формула суми перших n-членів геометричної прогресії
Опрацювати п. 19 стор.185 - 186.
Знати формулу суми геометричної прогресії.
Переглянути відео урок за посиланням:
Виконати№ 19.2 (1,3), №19.6
2 урок
ТЕМА УРОКУ: РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Самостійна робота
№ 1 Нехай (bn) дана геометрична прогресія. Знайти bІ2, якщо b1 = 25, b2 = - 50
№2 Знайти S9 даної геометричної прогресії: 1, -2, 4, -8,...
№3 Перший член геометричної прогресії дорівнює 3, а п'ятий 48. Скільки перших членів треба взяти, щоб їх сума дорівнювала 381.
№4. Між числами 2 і 162 вставте такі три числа, щоб вони разом з даними числами утворили геометричну прогресію.
Роботу виконувати у зошиті
Шановні учні сфотографуйте виконану самостійну роботу і надішлить на цю електронну адресу o.nebulutsia@gmail.com
Завдання виконати до 16.04.2020р.
Геометрія
14.04.2020 р.
1 урок
Тема уроку: Контрольна робота
Скористайтесь посиланням
https://naurok.com.ua/test/join?gamecode=796728
Вкажіть прізвище та ім'я
Приєднатися
Виконати до 21.04.2020р.
Розв'язки надсилайте
на цю електронну адресу o.nebulutsia@gmail.com
2 урок
Тема уроку: Переміщення ( рух) та його властивості. Паралельне перенесення.
Опрацювати п. 17
Переглянути відео уроки за посиланням:
https://www.youtube.com/watch?v=pARDH5aLQ08
Знати : що таке переміщення і його властивості; паралельне перенесення і формули паралельного перенесення.
16.04.2020 р.
Алгебра
1 урок
Тема уроку: Контрольна робота
1. ( 2 бали ). Знайдіть сьомий член і суму двадцяти перших членів арифметичної прогресії ( а n ), якщо а 1 = 4; d = - 2.
2. ( 2 бал ). Знайдіть три перших члени геометричної прогресії
( b n ), у якої b
1
= 6; q =
1,5.
Шановні учні сфотографуйте виконану контрольну роботу і надішлить на цю електронну адресу o.nebulutsia@gmail.com
2 урок
Тема: Основні правила комбінаторики
Опрацювати п.21
Знати правила суми та правила добутку.
Переглянути відео урок за посиланням:
https://www.youtube.com/watch?v=89hUMPho62c
Продивиться десь 10 хв. йде нова тема, а потім ідуть приклади розв'язання задач. Вам достатньо подивитись вивчення теми.
Виконати до 23.04.2020р.
Розв`язування систем лінійних нерівностей з однією змінною (натиснути тут)
Подвійні нерівності та нерівності з модулем (натиснути тут)
Розв`язування лінійних нерівностей з параметрами та задач за допомогою лінійних нерівностей (натинути тут)